ChaCha20-Poly1305の解説と実装

ChaCha20-Poly1305というAEAD暗号について、内部のアルゴリズムやPythonによる実装などを説明していきたいと思います。この記事を作るに当たって、@jovi0608 さんの記事新しいTLSの暗号方式ChaCha20-Poly1305 - ぼちぼち日記や、セキュリティ・キャンプ全国大会2018の「TLS 1.3/暗号ゼミ」の同じ参加者の @ykm_kn さんの記事 ChaCha20-Poly1305の解説と実装 - ぺんぎんさんのおうちを参考にしつつ、自分でもPythonで実装して理解したことを書いていきたいと思います。

なぜ ChaCha20-Poly1305 ?

2013年のEdward Snowdenの内部告発により、アメリカ国家安全保障局（NSA）の通信監視プログラム PRISM による広域監視が暴露され、その過程でアメリカ国立標準技術研究所（NIST）が「NIST SP 800-90A」で標準化した Dual_EC_DRBG という楕円曲線を使った乱数生成器にバックドアが仕掛けられていることが判明しました。このことにより、2つの動きが起こりました。

政府機関による監視への技術的対抗策を講じること（AEAD, forward secrecy などの利用）
政府機関により策定された暗号アルゴリズムの利用を避けること

インターネット技術の標準化を推進する IETF は中立性を尊重するので、IETF では NIST で採用されていない暗号アルゴリズムを標準化する動きが活発化しています。例えば、楕円曲線暗号におけるエドワーズ曲線（Ed25519）による鍵共有アルゴリズムや¹、この記事で説明する認証付き暗号の ChaCha20-Poly1305 などです²。このような流れの中で、IETF が標準化した ChaCha20-Poly1305 に注目が集まっています³。

ChaCha20-Poly1305 の概要

ChaCha20-Poly1305 は2つのモジュールから構成されています。

ChaCha20 : ストリーム暗号で暗号化する
Poly1305 : メッセージ認証コード (MAC; Message Authentication Code) を生成する

ChaCha20 と Poly1305 を組み合わせて、認証付き暗号（AEAD; Authenticated Encryption with Associated Data）を実現した暗号アルゴリズムが ChaCha20-Poly1305 です。具体的な仕様については IETF が RFC 8439 を発行しているので、具体的なアルゴリズムを知りたい場合は RFC を読んでください。

この記事では、ChaCha20 と Poly1305 の解説をした後に、ChaCha20-Poly1305 の全体像を解説していきたいと思います。

ChaCha20 とは

ChaCha20 はストリーム暗号で⁴、鍵ストリームを生成して平文と XOR することで暗号化を行うものです。ChaCha20 の入力と出力はそれぞれ以下の通りです。ただし、各要素は 32bit 整数です。

入力：
- 32byteの秘密鍵 $k = (\mathrm{key}_0, \mathrm{key}_1, …, \mathrm{key}_7)$
- 4byteのカウンタ $c = (\mathrm{counter}_0)$ … 初期値は 0x00000000
- 12byteのナンス $n = (\mathrm{nonce}_0, \mathrm{nonce}_1, \mathrm{nonce}_2)$
出力：
- 64byteの鍵ストリーム

ChaCha State

ChaCha20 には ChaCha State と呼ばれる内部状態があり、これを配列 $X$ で次のように表します。

\[X = \begin{bmatrix} x_0 & x_1 & x_2 & x_3 \\ x_4 & x_5 & x_6 & x_7 \\ x_8 & x_9 & x_{10} & x_{11} \\ x_{12} & x_{13} & x_{14} & x_{15} \\ \end{bmatrix} = \begin{bmatrix} \mathrm{const}_0 & \mathrm{const}_1 & \mathrm{const}_2 & \mathrm{const}_3 \\ \mathrm{key}_0 & \mathrm{key}_1 & \mathrm{key}_2 & \mathrm{key}_3 \\ \mathrm{key}_4 & \mathrm{key}_5 & \mathrm{key}_6 & \mathrm{key}_7 \\ \mathrm{counter}_0 & \mathrm{nonce}_0 & \mathrm{nonce}_1 & \mathrm{nonce}_2 \end{bmatrix}\]

ただし、const の部分はマジックナンバーで、次の定数値を使います⁵。

\[\begin{aligned} \mathrm{const}_0 &= \text{0x61707865} \\ \mathrm{const}_1 &= \text{0x3320646e} \\ \mathrm{const}_2 &= \text{0x79622d32} \\ \mathrm{const}_3 &= \text{0x6b206574} \\ \end{aligned}\]

Quarter Round

次に、QuarterRound という関数を使って内部状態の配列 $X$ を攪拌させます（かき混ぜます）。攪拌させることで鍵ストリームとして使えるランダムな文字列を得ることができます。 QuarterRound(a, b, c, d) 関数の擬似コードで次のように書くことができます。

a += b; d ^= a; d <<<= 16;
c += d; b ^= c; b <<<= 12;
a += b; d ^= a; d <<<= 8;
c += d; b ^= c; b <<<= 7;

図にすると次のようになります。⊞ は $2^{32}$ を法とする加算、⊕ は XOR、<<< n は n-bit 左巡回シフトを表しています。

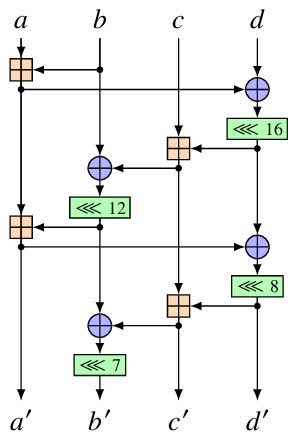
QuarterRound関数の内部では、加算、XOR、巡回シフトのみを用いるのでタイミング攻撃への耐性が高くなります。

QuarterRound関数は直訳すると1/4ラウンド関数となりますが、この1/4ラウンド関数を4回行うことで1ラウンドの処理を行います。なお、ラウンドは「奇数ラウンド」と「偶数ラウンド」に分けられ、それぞれ「列ラウンド」と「対角ラウンド」と呼ばれるラウンドの処理を行います。

# 列ラウンド：列の要素に対して行う
QuarterRound(x0, x4,  x8, x12)	# 1列目
QuarterRound(x1, x5,  x9, x13)	# 2列目
QuarterRound(x2, x6, x10, x14)	# 3列目
QuarterRound(x3, x7, x11, x15)	# 4列目

# 対角ラウンド：対角線の要素に対して行う
QuarterRound(x0, x5, x10, x15)	# 1番目の対角線
QuarterRound(x1, x6, x11, x12)	# 2番目の対角線
QuarterRound(x2, x7,  x8, x13)	# 3番目の対角線
QuarterRound(x3, x4,  x9, x14)	# 4番目の対角線

列ラウンドと対角ラウンドを図で表すと次のようになります。

「列ラウンド」と「対角ラウンド」を合わせて「ダブルラウンド」と呼び、ダブルラウンドを10回行う（各ラウンドは合計で20回行う）ことで内部状態の配列の攪拌を行います。

最後に、内部状態の「攪拌する前の配列 $X$」と「攪拌した後の配列 $X'$」の各要素を $2^{32}$ を法として加算をして、バイト列に変換した結果が、ChaCha20 の出力する鍵ストリームとなります。そして、鍵ストリームと平文 $M$ を XOR することで、暗号文 $C$ を得ることができます。

Poly1305 とは

Poly1305 はメッセージ認証コード (MAC) を生成するものです。 Poly1305 の入力と出力はそれぞれ以下の通りです。

入力
- 認証するデータ $C = (c_1, c_2, …, c_n)$ … 16byteごとに区切ったもの
- 32byteの鍵 $K = (r, s)$ … それぞれ 16byte
出力
- 16byteの認証タグ $T$

Poly1305 は名前にもなっているように、多項式 (Polynomial) を使って認証タグを計算して求めます（つまり $T = f(r)$ となります）。Poly1305 の多項式 $f(r)$ は次の形式になっています。ただし、各係数 $c'_i$ は、もとのバイト列 $c_i$ にバイト列 0x01 を加えたものです。また、Poly1305関数の入出力はバイト列でしたが、内部では数学的な計算を行うので、それぞれの要素（$c'_i, r, s$）は、le_bytes_to_num 関数によってバイト列から整数に変換されています。

\[\begin{aligned} c_i &\leftarrow \text{le\_bytes\_to\_num}(c_i \;||\; 01) \\ r &\leftarrow \text{le\_bytes\_to\_num}(r) \\ r &\leftarrow \text{clamp}(r) \\ s &\leftarrow \text{le\_bytes\_to\_num}(s) \end{aligned}\] \[f(r) = ((c_1 r^n + c_2 r^{n-1} + \cdots + c_{n-1} r^2 + c_n r^1) \;\mathrm{mod}\;2^{130}-5) + s\]

なお、上記の式は、ホーナー法を使うことでより簡単に認証タグを計算することができます。

\[f(r) = (((\dots(c_1 r + c_2)r + \dots + c_{n-1})r + c_n)r \;\mathrm{mod}\;2^{130}-5) + s\]

次に、認証タグの計算で使われる関数の説明をします。

le_bytes_to_num 関数は、リトルエンディアン（左側から小さい桁を表す形式）のバイト列を整数に変換する関数です。 le_bytes_to_num 関数の簡単な動作例を Python で書き表すと次のようになります。
```
  le_bytes_to_num(b'\x01\x00')  # => 1
  le_bytes_to_num(b'\x00\x01')  # => 256
```
$\text{clamp}$ 関数は、与えられた整数をビット列で表すとき、途中のビット（合計22ビット）を0にする関数です。 Pythonでは次のように実装します。
```
  def clamp(r: int) -> int:
      return r & 0x0ffffffc0ffffffc0ffffffc0fffffff
```

最後に、多項式 $f(r)$ を計算した結果の値を16byteのバイト列に変換します (オーバーフローしている分は無視します)。こうして得られたバイト列が認証タグ $T$ となります。

ChaCha20-Poly1305 とは

ChaCha20-Poly1305 とは ChaCha20 と Poly1305 を組み合わせた認証付き暗号（AEAD）のことです。具体的には「暗号化と認証タグ生成」と「復号と認証タグ検証」の2つの機能があります。

暗号化と認証タグ生成

ChaCha20-Poly1305 の暗号化と認証タグ生成における、入力と出力はそれぞれ以下の通りです。

入力
- 32byteの鍵 $K$
- 12byteのナンス $\mathrm{Nonce}$
- 平文 $M$
- AAD (追加の認証データ) … これまでの通信内容から両者がすでに知っている情報が使われる。例えば TLS 1.3 では、暗号化した送信データの長さなどが使われる。
出力：
- 暗号文 $C$
- 16byteの認証タグ $T$

暗号化と認証タグ生成の流れを書くと、次のようになります。

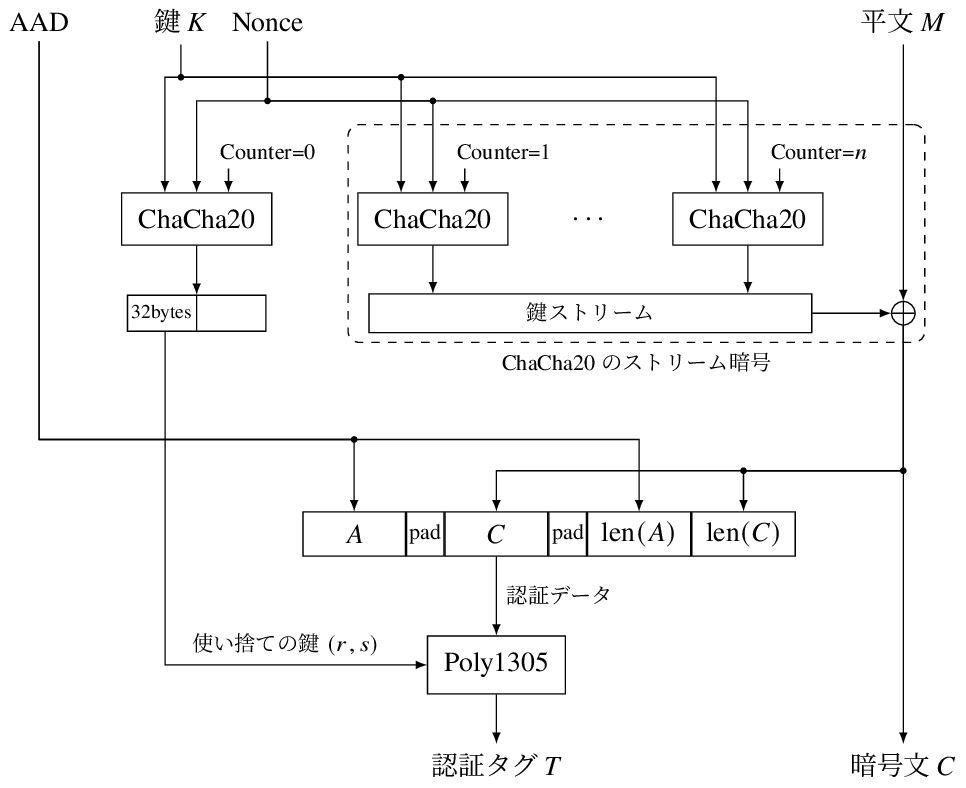
ChaCha20のストリーム暗号で平文を暗号化する部分がありますが、カウンター（Counter）を1から開始して暗号化を行います。カウンターが0のときの鍵ストリームは、左側の32byteを Poly1305 の鍵として利用します。

Poly1305 に与える認証データは次の6つから構成されます。ただし「長さ」は「byte数」のことを意味します。

$\text{AAD}$ … 追加の認証データ
$\text{pad}(\text{AAD})$ … 追加の認証データの長さを16の倍数にするための0パディング
$C$ … 暗号文
$\text{pad}(C)$ … 暗号文の長さを16の倍数にするための0パディング
$\text{len}(\text{AAD})$ … 追加の認証データの長さ
$\text{len}(C)$ … 暗号文の長さ

ここまでは ChaCha20-Poly1305 による暗号文と認証タグの出力の流れについてでした。次は ChaCha20-Poly1305 による復号と検証について説明していきます。

復号と認証タグ検証

ChaCha20-Poly1305 の復号と認証タグの検証は、ほとんど暗号化のときと同じです。入力と出力はそれぞれ以下の通りです。

入力
- 32byteの鍵 $K$
- 12byteのナンス $\mathrm{Nonce}$
- 暗号文 $C$
- 認証タグ $T$
- AAD (追加の認証データ) … これまでの通信内容から両者がすでに知っている情報が使われる
出力：
- 検証結果が真のとき、平文 $M$
- 検証結果が偽のとき、復号失敗のエラー

復号と認証タグ検証の流れを書くと、次のようになります。暗号化とタグ生成のときと違うところは、図の右側と右下あたりです。

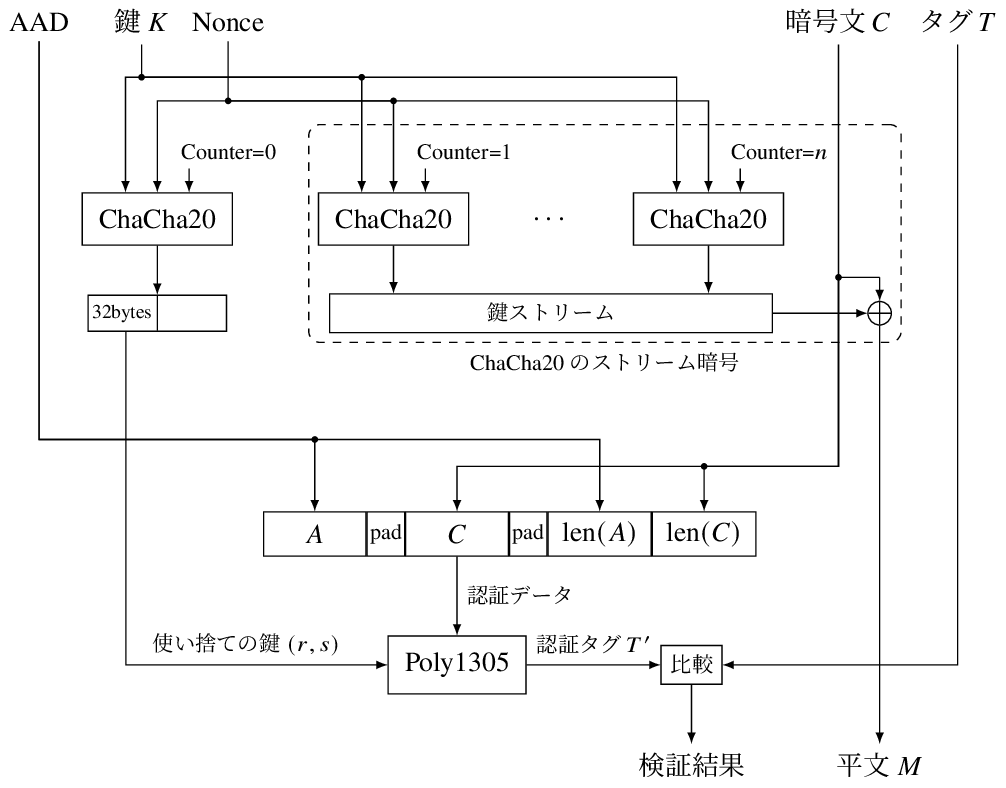
入力された暗号文は ChaCha20 の鍵ストリームと XOR されて平文になります。さらに、入力された暗号文は改竄されていないか（パディングオラクル攻撃など）を確認するための Poly1305 による認証が行われます。これが ChaCha20-Poly1305 の AEAD (認証付き暗号) としての機能です。

Python による実装

ここまで、ChaCha20-Poly1305 の概要について説明しましたが、細かいところ（バイト列と整数の変換方法など）は説明していません。具体的な仕様や擬似コードによる説明は ChaCha20 and Poly1305 for IETF Protocols (RFC 8439) に書かれているので、こちらを一読していただくのが確実だと思います。注意ですが、同じタイトルで RFC 7539 もありますが、こちらは間違いが7個あり、間違いを訂正してセキュリティの考慮事項 (Security Considerations) の章を追加したのが RFC 8439 となります。 HTML版のRFCでは上部に色の帯があり、これが茶色になっていると廃止されたRFCを見ていることがわかるので、RFCを読むときは色の部分にも注目してください。

私が書いた ChaCha20-Poly1305 の Python プログラムは GitHub にて公開しています。ご自由にご利用ください。

　tex2e/chacha20-poly1305: ChaCha20 and Poly1305 for IETF Protocols (RFC 8439)

なお、プログラム内には RFC 8439 内のテストベクタが全て入っていますので、 python chacha20.py のように実行するとテストが実行されます。

以上です。

エドワーズ曲線（Ed25519）による鍵共有アルゴリズムなどについての RFC : Elliptic Curves for Security - RFC 7748 ↩
ChaCha20 and Poly1305 for IETF Protocols (RFC 8439) ↩
ChaCha20-Poly1305の実装性能調査 - 株式会社レピダム ↩
シャーロックホームズには「踊る人形」という暗号があり、踊ることからダンスが連想されるので、暗号アルゴリズムに名前を付けるときにダンスが由来の単語（SalSa、ChaCha、Rumba など）が使われるとか ↩
ChaCha20 の定数値 $\text{const} = (\text{0x61707865}, \text{0x3320646e}, \text{0x79622d32}, \text{0x6b206574})$ は「expand 32-byte k」という ASCIIで書かれた16文字の文を 4つの32bit整数にリトルエンディアンでアンパックさせたものです。次のPythonプログラムで導出することができます。
```
import struct
print([hex(x) for x in struct.unpack('<IIII', b'expand 32-byte k')])
# => ['0x61707865', '0x3320646e', '0x79622d32', '0x6b206574']
```
このような定数値は Nothing-up-my-sleeve number の一例と言えます ↩

晴耕雨読

working in the fields on fine days and reading books on rainy days