剰余の乗法の逆元とRSA暗号

内容は剰余の乗法の逆元（モジュラ逆数）についてです。 CTFをやると、RSA暗号の秘密鍵を解く問題で、次のようなWriteupを見たことがあるかと思います。

import libnum

e = 65537
p = 12476682960795779723419989287306239606331347310604553825605263028855086418051086300006278888049896375754096827163121306696417314531666670662341673511789487
q = 10626608485185909739187126602183513204215955466032868268570782358820047751795982373252873333276843831383542360202874683262678664975380865415068554992090483
c = 126028558760741438230925566962334702896791270808414391828894437291120207835997354509410869568173448979784329516392078311028442458946906210498176026685581176779209904039179175088984829699783861789249260322822491502790157863487861171337660785254139478229397872969136220001367017765809130698515063339265165085655

N = p*q
phi = (p-1)*(q-1)
d = libnum.modular.invmod(e, phi)  # 秘密鍵を求める処理
print(libnum.n2s(pow(c, d, N)))

いわゆる、$N$ が素因数分解で $p \times q$ にできたら秘密鍵 $d$ は計算できるというやつですが、ここで出てくるメソッド libnum.modular.invmod() は数学では何をしているか説明したいと思います。

まず結論からいうと、invmod(e, phi)は次のように書き換えることができます。

\[\begin{aligned} d &\equiv \mathrm{invmod}(e, \phi) \\ d &\equiv e^{-1} \pmod{\phi} \end{aligned}\]

ただし、$d$, $e$, $\phi$は整数です。ここで剰余演算について詳しく知らない人は「逆数の剰余って計算できるの？」と疑問に思います。おそらく疑問に思っているところは次の点だと思います。例えば $e = 7, \phi = 5$ として、 $\gdef\mod{ {\;\mathrm{mod}\;} }$

$7$ の逆数は $7^{-1} = \dfrac{1}{7}$ （有理数）
$7$を$5$で割った余りは $7 \mod 5$ で答えは $2$ （剰余演算は整数のみ）

なので、$7^{-1} \pmod{5}$ は一見すると有理数の剰余演算に見えるので、計算できないのではないかと思ってしまいます。

1. 剰余と合同式

まず、数学のおさらいをしていきたいと思います。 C言語などでは % 演算子で剰余を求めることができますが、改めて剰余の定義を数式で定義しておきましょう。

余りの定義

$a$ を $b$ で割ったときの商 $q$ と余り $r$ を次のように表す。ただし、$a,b$ は自然数、$q,r$ は自然数または $0$ とする。
\[a = bq + r \;\;\;(0 \le r < b) \tag{1.1}\]
剰余の定義

整数 $a,b,q,r$ で、$b \ne 0$ とする。
\[a \mod b = r \;\Longleftrightarrow\; a = bq + r \;\;\;(0 \le r < |b|) \tag{1.2}\]

要するに、自然数の余りの定義を整数に広げたものが剰余（$\mathrm{mod}$）です。例えば $7 \mod (-3)$ の答えは何になるでしょうか？式(1.2)に沿って置き換えると以下のようになります。

\[7 \mod (-3) = r \Longleftrightarrow 7 = (-3) q + r \;\;\;(0 \le r < \lvert -3\rvert)\]

条件 $0 \le r < 3$ の下で、整数 $q = -2, r = 1$ とすると $7 = (-3)(-2) + 1$ となり上式を満たすので、答えは $7 \mod (-3) = 1$ となります。余談ですが、プログラミング言語によって剰余の結果は異なります。

剰余の次は合同式について説明します。

合同式の定義

$a,b$ を $c$ で割った余りが等しいとき「$a,b$ は $c$ を法として合同」といい、次のように表す。
\[a \equiv b \pmod{c} \tag{1.3}\]

合同式の加算・減算・乗算は一般的な等式と同じです。

\[\begin{aligned} a + C &\equiv b + C \pmod N \\ a - C &\equiv b - C \pmod N \\ a \times C &\equiv b \times C \pmod N \end{aligned}\]

ただし、合同式の除算はできる場合とできない場合があります。除算ができる条件は、割る数 $C$ と法 $N$ が互いに素であること（$C$ と $N$ の最大公約数が$1$であること）です。

\[a \div C \equiv b \div C \pmod N \;\;\;\;\; (C \bot N)\]

除算できない例（割る数 $3$ と法 $6$ が互いに素ではない）：

\[\begin{aligned} 9 &\equiv 21 \pmod 6 \\ 3 &\not\equiv 7 \pmod 6 \end{aligned}\]

除算できる例（割る数 $3$ と法 $5$ が互いに素）：

\[\begin{aligned} 51 &\equiv 21 \pmod{5} \\ 17 &\equiv 7 \pmod{5} \end{aligned}\]

この「割る数」と「法」が互いに素であるという条件は、合同式の除算が可能になるだけではなくて、乗算の逆元の存在を示す十分条件にもなります。

2. 剰余の乗算の逆元

ここからは「割り算をする」を「逆数を掛け算する」と捉えることにします。そこでまず、乗算の逆元を理解するには単位元と逆元について理解する必要があります。なお、集合の「元」とは集合の「要素」と同じ意味です。

単位元の定義

集合 $G$ の任意の元 $a$ に対して、以下の式を満たす集合 $G$ の元 $e$ を、演算 $\circ$ における単位元と呼ぶ。
\[a \circ e = e \circ a = a \tag{2.1}\]

例えば、整数全体の集合 $\mathbb{Z}$ の加算における単位元は $0$ で、乗算における単位元は $1$ です。

逆元の定義

$a$ を集合 $G$ の元とし、$e$ を単位元とする。$a$ に対して以下の式を満たす $b \in G$ を、演算 $\circ$ に関する $a$ の逆元と呼ぶ。
\[a \circ b = b \circ a = e \tag{2.2}\]

例えば、整数全体の集合 $\mathbb{Z}$ の加算では$3$の逆元は$-3$になりますが、$\mathbb{Z}$ の乗算では $4 \times b = 1$ を満たす整数 $b$ は存在しないので、乗算の逆元は存在しません。集合を有理数全体の集合 $\mathbb{Q}$ にすると$4$の乗算の逆元は存在し、$4^{-1} = \frac{1}{4}$となります。

ここで、剰余の$\pmod{N}$ の世界でも逆元が定義できれば一番最初の疑問を解くことができそうです。つまり $7 \times b \equiv 1 \pmod 5$ を満たす整数 $b$ があるとすれば、$b \equiv 7^{-1} \pmod 5$ となるので、$b$ は $7$ の逆元であると言えます。

なお、$\pmod{N}$ の世界を集合で表すときは、この集合を剰余環と呼び、

\[\mathbb{Z}/N\mathbb{Z} = \{0,1,2,...,N-1\}\]

と書きます。例えば、$\pmod{5}$ の世界は集合で次のように表せます。

\[\mathbb{Z}/5\mathbb{Z} = \{0,1,2,3,4\}\]

剰余環は環の性質を持っています。なので、剰余の加算・乗算は整数の加算・乗算とほとんど変わりません。

群の定義

以下の公理（axiom）を満たす集合 $G$ を群（Group）と呼ぶ。
1. 演算 $*$ に関して閉じている（$\forall a,b \in G,\; a * b \in G$）
2. 任意の元に対して、結合法則が成立する（$\forall a,b,c \in G,\; a*(b*c) = (a*b)*c$）
3. 単位元が存在する（$\forall a \in G, \exists e \in G,\; a*e=e*a=a$）
4. 任意の元に対して、逆元が存在する（$\forall a \in G, \exists b \in G,\; a*b=b*a=e$）
環の定義

加法 $+$ および乗法 $\times$ が定義された以下の公理を満たす集合 $R$ を環（Ring）と呼ぶ。
1. 加法の下に可換群（交換則 $a*b = b*a$ が成立する群）である
2. 乗法 $\times$ に関して閉じている（$\forall a,b \in G,\; a \times b \in G$）
3. 任意の元に対して、乗法の結合則が成立（$\forall a,b,c \in G,\; a\times (b\times c) = (a\times b)\times c$）
4. 任意の元$a,b,c$に対して、以下の分配法則が成立する
\[a \times (b + c) = a \times b + a \times c \tag{2.3}\] \[(b + c) \times a = b \times a + c \times a \tag{2.4}\]

では、集合 $\mathbb{Z}/5\mathbb{Z}$ における $2\pmod{5}$ の逆元である $2^{-1}\pmod{5}$ とは一体何でしょうか？集合は $\mathbb{Z}/5\mathbb{Z} = \{0,1,2,3,4\}$ なので、全部の値をそれぞれ掛け合わせてみて乗法の単位元の $1$ になるか計算してみましょう。

\[\begin{aligned} (2 \;(\mathrm{mod}\; 5)) \times (0 \;(\mathrm{mod}\; 5)) \;\;\; &= 0 \;(\mathrm{mod}\; 5) &\equiv 0 \\ (2 \;(\mathrm{mod}\; 5)) \times (1 \;(\mathrm{mod}\; 5)) \;\;\; &= 2 \;(\mathrm{mod}\; 5) &\equiv 2 \\ (2 \;(\mathrm{mod}\; 5)) \times (2 \;(\mathrm{mod}\; 5)) \;\;\; &= 4 \;(\mathrm{mod}\; 5) &\equiv 4 \\ (2 \;(\mathrm{mod}\; 5)) \times (3 \;(\mathrm{mod}\; 5)) \;\;\; &= 6 \;(\mathrm{mod}\; 5) &\equiv 1 \\ (2 \;(\mathrm{mod}\; 5)) \times (4 \;(\mathrm{mod}\; 5)) \;\;\; &= 8 \;(\mathrm{mod}\; 5) &\equiv 3 \\ \end{aligned}\]

$\mathbb{Z}/5\mathbb{Z}$ では$2$に$3$を掛けると乗法の単位元 $1$ となることから、 $2 \pmod 5$ の逆元は $3 \pmod 5$ であることがわかりました。

\[\begin{aligned} 2^{-1} \;(\mathrm{mod}\; 5) &= 3 \;(\mathrm{mod}\; 5) \\ &\equiv 3 \end{aligned}\]

$2$と$7$は$5$を法として合同なので、$2$と$7$の逆元も同じになります。

\[\begin{aligned} 7^{-1} \;(\mathrm{mod}\; 5) &= (7 \;(\mathrm{mod}\; 5))^{-1} \\ &= (2 \;(\mathrm{mod}\; 5))^{-1} \\ &= 2^{-1} \;(\mathrm{mod}\; 5) \\ &= 3 \;(\mathrm{mod}\; 5) \\ &\equiv 3 \end{aligned}\]

では、$0$は何を掛けても$0$になるので除くとして、集合 $\mathbb{Z}/5\mathbb{Z}$ から$0$を除いた集合 $(\mathbb{Z}/5\mathbb{Z})^*$ の任意の元について、乗算の逆元は存在すると言えるのでしょうか？ $\mathbb{Z}/4\mathbb{Z}$ と $\mathbb{Z}/5\mathbb{Z}$ についてそれぞれの乗算の結果をまとめた表を以下に示します。この表のことを演算表と呼び、乗算についての演算表を乗算表と呼んだりします。

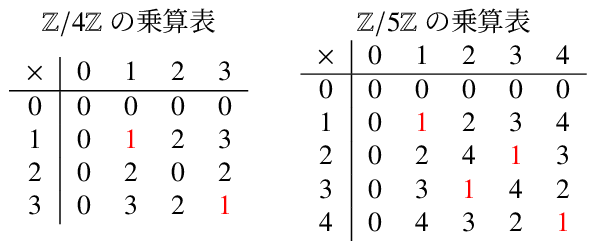
そうすると、乗算表からわかるように $(\mathbb{Z}/5\mathbb{Z})^*$ の全ての元には逆元が存在する（つまり乗算したら$1$になる元が存在する）ことが確認できますが、$(\mathbb{Z}/4\mathbb{Z})^*$ の元である $2$ は任意の元と掛け合わせても$1$にならないので逆元は存在しないことになります。

それでは、どのような条件を満たす時に $(\mathbb{Z}/N\mathbb{Z})^*$ の全ての元に逆元が存在すると言えるのでしょうか？ここで合同式の除算ができる条件を思い出すと「割る数 $C$ と法 $N$ が互いに素であること」でした。つまり、任意の元で除算ができる、すなわち逆元が存在することを示すには、集合 $(\mathbb{Z}/N\mathbb{Z})^* = \{1,2,\ldots,N-1\}$ のそれぞれの元 $1,2,\ldots,N-1$ が法 $N$ と互いに素であることが条件になります。この条件を満たす法 $N$ は素数しかないのです。

$p$ を素数とすると、剰余環 $\mathbb{Z}/p\mathbb{Z}$ の全ての元について逆元が存在します。この集合を体といい、素数 $p$ を法とする剰余環 $\mathbb{Z}/p\mathbb{Z}$ を有限体と呼びます。

\[\mathbb{F}_p = \mathbb{Z}/p\mathbb{Z} \;\;\;\;\; (p \;\text{is a prime})\]

体の定義

加法 $+$ および乗法 $\times$ が定義された以下の公理を満たす集合 $K$ を体（field）と呼ぶ。
1. 加法の下に可換群である
2. $K$ から加法の単位元 $0$ を除いた集合 $K^* = K \setminus \{0\}$ は乗法に関して可換群である
3. 分配法則が成立する

ちなみに、RSA暗号に関して言えば有限体は全く出てこないので知らなくても問題ないですが、せっかく剰余環について書いたので有限体にも触れておこうかなと思った次第です。ここまでで剰余の乗算の逆元について説明してきたので、次はいよいよRSAの話をしたいと思います。

3. RSA暗号方式の鍵生成

逆元を求めるために毎回乗算表を作っていたら大変ですよね。実際、秘密鍵を作るときは大きな数（例えば600桁）を使うので、乗算表を作っていたら日が暮れてしまいます。では、RSAの鍵生成ではどのように秘密鍵を作っているか確認してみましょう。 RSA暗号のアルゴリズムは次のように定義されています。

RSA：鍵生成
1. 二つの大きな素数 $p, q$ を適切に決める。
2. $N = pq$ を求める。
3. オイラーの関数 $\varphi(N) = (p-1)(q-1)$ を計算する。
4. 整数 $e$ を $\varphi(N)$ 未満の正の整数で、 $\varphi(N)$ と互いに素な数とする。
5. 公開鍵を $n, e$ とする。
6. 秘密鍵 $d$ を、$\varphi(N)$ を法とした $e$ の逆数（$ed \equiv 1 \pmod{\varphi(N)}$）とする。$d$ は拡張ユークリッドの互除法を使えば容易に求まる。
RSA：暗号化

$m$ を平文空間 $\mathbb{Z}_n = \{0,1,2,\ldots,n-1\}$ の元とすると、暗号文 $c$ は次の式で求まる。
\[c = m^e \mod n \tag{3.1}\]
RSA：復号

$c$ を暗号文とすると、平文 $m$ は次の式で求まる。
\[m = c^d \mod n \tag{3.2}\]

鍵生成のところで $ed \equiv 1 \pmod{\varphi(N)}$ と書かれているのは $e \equiv d^{-1} \pmod{\varphi(N)}$ と同じ式です。 $\varphi(N)$ とはオイラーの関数で、$1$ から $N$ までの自然数のうち $N$ と互いに素なものの個数を返す関数のことです。例えば、$N$ が素数なら $1$ から $N-1$ までの自然数の全てと互いに素なので、$\varphi(N) = N-1$となります。また、オイラーの関数は互いに素な数の積に関して乗法的であるので、$N$ が二つの素数の合成数 $N = pq$ の場合は $\varphi(N) = (p-1)(q-1)$ が成り立ちます。

RSA暗号の安全性は素因数分解の困難性に依拠しています。「依拠する」とは暗号の解読それらの問題の困難さとの間に厳密な等価性が成り立つという意味ではなく、ただ頼っているという意味です。 $N$ の素因数を知らない解読者は、法 $\varphi(N)$ を知らないので、ユークリッドの互除法を使えず、秘密鍵は求められません。しかし今後コンピュータの性能が向上して $N$ の素因数分解が現実的な時間でできるようになったとき、簡単に $N$ は素因数分解されて秘密鍵 $d$ は計算で求められてしまっては困ります。なので、今使っているRSAのビット数が心配という方は、CRYPTRECが公表している『CRYPTREC暗号リスト（電子政府推奨暗号リスト）』に一度目を通しておくと良いです。

RSAの暗号化して復号したときの結果が等しくなることはオイラーの定理 $a^{\varphi(n)} \equiv 1 \pmod{n}$ を使うと簡単に説明できます（ただし、$m < n$ とする）。

\[\begin{aligned} m &= c^d \mod n = (m^e \mod n)^d \mod n \\ &= m^{ed} \mod n = m^{1 + k \varphi(n)} \mod n \\ &= m^1 \cdot{} m^{k\varphi(n)} \mod n = m \cdot{} 1 \mod n = m \end{aligned}\]

話を戻して、秘密鍵 $d$ は拡張ユークリッドの互除法を使うと（乗算表を使わなくても）簡単に求めることができます。それでは次は拡張ユークリッドの互除法の話でもしたいと思います。

4. 拡張ユークリッドの互除法による invmod

冒頭に示したメソッド invmod は拡張ユークリッドの互除法を使うことで簡単に求めることができます。そこで、ユークリッドの互除法と拡張ユークリッドの互除法について説明したいと思います。

4.1. ユークリッドの互除法

拡張ユークリッドの互除法の前に、ユークリッドの互除法の説明を簡単にしておきます。ユークリッドの互除法とは最大公約数を求めるアルゴリズムです。余りの定義(1.1)より、$a$ を $b$ で割った商 $q$ と余り $r$ とすると、$a$ は $a = bq + r$ のように表すことができます。

$r = 0$ のときは明らかに $a$ と $b$ の最大公約数 $\gcd(a,b)$ は $b$ となります。 $r \ne 0$ のときは $r = a - bq$ と表せるので、$\gcd(a,b)$ は $r$ の約数です。なので $\gcd(b,r) \le \gcd(a,b)$ となります。一方、$a = bq + r$ と表されるから、$a$ は $\gcd(b,r)$ の約数です。なので $\gcd(b,r) \ge \gcd(a, b)$ となります。したがって、$\gcd(b,r) = \gcd(a,b)$ となるので、$\gcd(b,r)$ を求めることは $\gcd(a,b)$ を求めることと同じということになります。 $(a,b)$ よりも $(b,r)$ の方が小さい整数の組なので、当然 $\gcd(a,b)$ よりも $\gcd(b,r)$ を求める方が簡単です。説明を端折りますが、この処理を繰り返していって $r = 0$ となったときの $b$ が求めるべき最大公約数となります。最大公約数を求めるプログラムをPythonで書くと下のようになります。

def gcd(a, b):
    while b != 0:
        a, b = b, a % b
    return a

4.2. 拡張ユークリッドの互除法

ユークリッドの互除法の応用として、拡張ユークリッドの互除法というアルゴリズムがあります。拡張ユークリッドの互除法は $a,b$ を正の整数とすると、次のベズーの等式を満たす適当な整数 $x,y$ が存在するので、この $x,y$ を求めるアルゴリズムです。

\[ax + by = \gcd(a,b)\]

ユークリッドの互除法において、その $k$ 回目の除算の商を $q_k$、余りを $r_k$ とすると、ユークリッドの互除法は以下のように書くことができます。ただし $r_k = 0$ になったときにユークリッドの互除法は終了します。

\[\begin{aligned} r_1 &= a - q_1 b \\ r_2 &= b - q_2 r_1 \\ r_3 &= r_1 - q_3 r_2 \\ r_4 &= r_2 - q_4 r_3 \\ &\;\;\vdots \\ r_k &= r_{k-1} - q_k r_{k-1} \\ &\;\;\vdots \end{aligned}\]

この式の右辺にある $r_{k-2}, r_{k-1}$ を上の式で消去していくと、$r_k$ は整数を係数とする $a$ と $b$ の線型結合で表すことができます。例えば $r_1$ と $r_2$ について $a$ と $b$ の式に書き換えると次のようになります。

\[\begin{aligned} r_1 &= 1 \cdot{} a + (- q_1) b \\ r_2 &= b - q_2 r_1 = (-q_2)a + (1 + q_2 q_1)b \\ \end{aligned}\]

$r_i = x_i a + y_i b$ と表すことにすると、上式より $x_1 = 1,\; y_1 = -q_1,\; x_2 = -q_2,\; y2 = 1 + q_2 q_1$ となります。そこで、$i < k$ を満たす $i$ について $r_i$ を表すと

\[\begin{aligned} r_k &= r_{k-2} - q_k r_{k-1} \\ &= (x_{k-2} a + y_{k-2} b) - q_k (x_{k-1} a + y_{k-1} b) \\ &= (x_{k-2} - q_k x_{k-1}) a + (y_{k-2} - q_k y_{k-1}) b \\ &= x_k a + y_k b \end{aligned}\]

より、$x_k, y_k$ は次式になります。

\[\begin{aligned} x_k &= x_{k-2} - q_k x_{k-1} \\ y_k &= y_{k-2} - q_k y_{k-1} \end{aligned}\]

初期条件を $x_0 = 1, y_0 = 0, x_0 = 0, x_1 = 1$ としてユークリッドの互除法でその都度求まる $q_k$ を使って $x_i, y_i$ を計算していけば、$\gcd(a,b) = r_n = x_n a + y_n b$ を満たす $x_n, y_n$ を求めることができます。そして、このときの $x_n, y_n$ が求めるべき $x, y$ となります。

拡張ユークリッド互助法のアルゴリズムをPythonで書くと次の通りです。この関数の返り値は (最大公約数$\gcd(a,b)$の値, 整数$x$, 整数$y$) です。

def xgcd(a, b):
    x0, y0, x1, y1 = 1, 0, 0, 1
    while b != 0:
        q, a, b = a // b, b, a % b
        x0, x1 = x1, x0 - q * x1
        y0, y1 = y1, y0 - q * y1
    return a, x0, y0

4.3. 剰余環の乗法逆元

剰余の乗法の逆元（invmod）は拡張ユークリッドの互除法を使って求めます。もし $a$ には法 $m$ の乗法逆元が存在するなら、二つの整数 $a, m$ の最大公約数 $\gcd(a,m)$ は $1$ になります。すなわち、拡張ユークリッドの互除法で出てきたベズーの等式を使うと、次式が成り立ちます。

\[ax + my = \gcd(a,m) = 1\]

書き換えると

\[ax = 1 + (-y)m\]

つまり

\[ax \equiv 1 \pmod{m}\]

となるので、拡張ユークリッドの互除法を計算することで $a$ の乗法逆元 $x$ を求めることができます。

Pythonで書くと下のようになります。

def invmod(a, m):
    g, x, y = xgcd(a, m)
    if g != 1:
        raise Exception('modular inverse does not exist')
    else:
        return x % m

試しに計算させてみましょう。手で計算した $7^{-1} \;(\mathrm{mod}\; 5)$ や、$\mathbb{Z}/4\mathbb{Z}$ の乗算表から逆元が存在しないことがわかっている $2^{-1} \;(\mathrm{mod}\; 4)$ を試してみます。

>>> invmod(7, 5)
3
>>> invmod(2, 4)
Exception: modular inverse does not exist

正しく計算できているようです。

という訳で invmod もとい、剰余の乗法の逆元を求める話はこの辺で終わりにしたいと思います。最後までお付き合い頂きありがとうございました。

晴耕雨読

working in the fields on fine days and reading books on rainy days