公開鍵暗号の安全性のレベルは、「攻撃モデル」と「解読モデル」の組み合わせで決定されます1。
攻撃モデル
攻撃モデルを弱い順に並べると以下のようになります2。 調べれば他にもありますが省略。
- 暗号文単独攻撃 (Ciphertext-only attack; COA):暗号文のみが得られるモデル
- 既知平文攻撃 (Known-plaintext attack; KPA):限られた数の平文と暗号文のペアが得られるモデル
- 選択平文攻撃 (Chosen-plaintext attack; CPA):任意の平文に対して暗号文が得られるモデル(暗号化オラクル)
- 適応的選択平文攻撃 (Adaptive chosen-plaintext attack; CPA2):CPAで平文を選ぶときに以前の暗号化の結果を使うことができるモデル
- 選択暗号文攻撃 (Chosen-ciphertext attack; CCA, CCA1):任意の暗号文に対して平文が得られるモデル(復号オラクル)
- 適応的選択暗号文攻撃 (Adaptive chosen-ciphertext attack; CCA2):CCAで暗号文を選ぶときに以前の復号の結果を使うことができるモデル
解読モデル
解読モデルを易しい順に並べると以下のようになります。ただし、強秘匿性(SS)と識別不可能性(IND)は等価であることが知られています1 3。
- 一方向性 (Onewayness; OW):暗号文から平文を求めるのは困難
- 強秘匿性 (Semantic Security; SS):暗号文から平文のどのような部分情報も得ることは困難
- 識別不可能性 (Indistinguishability; IND):暗号文 $m_0, m_1$ が平文 $c_0, c_1$ のどちらを暗号化したものか識別できない4
- 頑強性 (Non-Malleability; NM):暗号文が与えられたとき、ある関係性を持った別の暗号文の生成ができない5
公開鍵暗号の安全性の関係
公開鍵暗号の安全性の関係を以下に示します1 6。 図の矢印は、例えば $A \Rightarrow B$ のとき、$A$の安全性を満たせば$B$の安全性も満たすことを示しています。
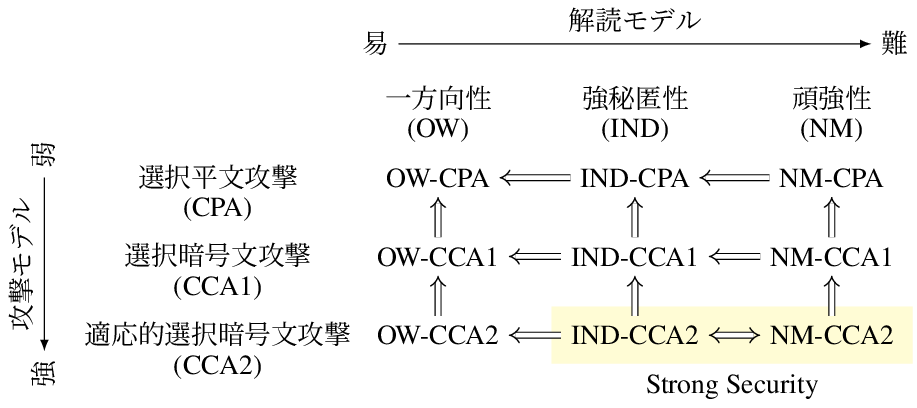
NMの条件は論理的に扱うのが難しいため、NM-CCA2の代わりにIND-CCA2の安全性を満たしているか検証することで、公開鍵暗号の安全性を保証することができます。 なので、公開鍵暗号を設計するときには、IND-CCA2安全を満たすことが目標の1つになります。