楕円曲線は連続で滑らかな曲線ですが、楕円曲線を有限体で考えると楕円曲線は曲線ではなく点の集まりになります。つまり、楕円曲線暗号で使う楕円曲線は、楕円でもないし曲線でもないです。ここでは、有限体上の楕円曲線についてパラメータを様々なものに変更したものをグラフにして眺めてみたいと思います。

補足：楕円曲線上の加算や2倍算のグラフを見たい方は「楕円曲線上の加算・2倍算のグラフを作成する」をご覧ください。

楕円曲線 $y^2 \equiv x^3 + x + 1$

$a=1,\;b=1$ のときの、グラフ描画用のSageMathコードと、結果のグラフを示します。

実数体 $\mathbb{R}$ 上

EllipticCurve([1,1]).plot()

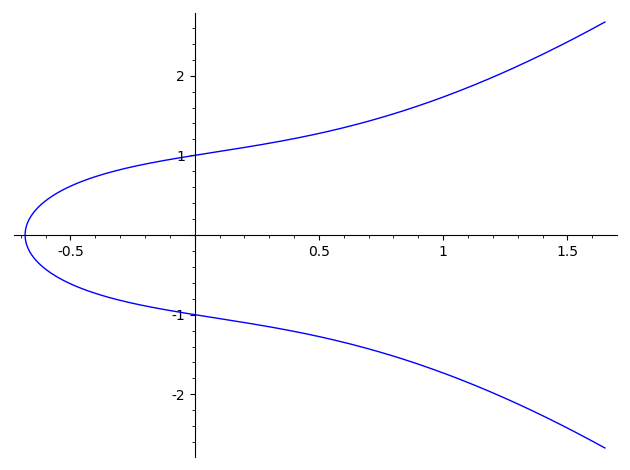
有限体 $\mathbb{F}_{23}$ 上

\(y^2 \equiv x^3 + x + 1 \pmod{23}\)

EllipticCurve(GF(23), [1,1]).plot()

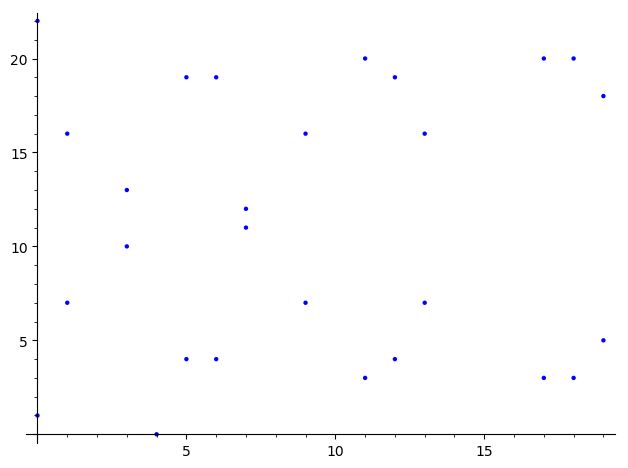
楕円曲線 $y^2 \equiv x^3 - 2x + 0$

$a=-2,\;b=0$ のときの、グラフ描画用のSageMathコードと、結果のグラフを示します。

実数体 $\mathbb{R}$ 上

EllipticCurve([-2,0]).plot()

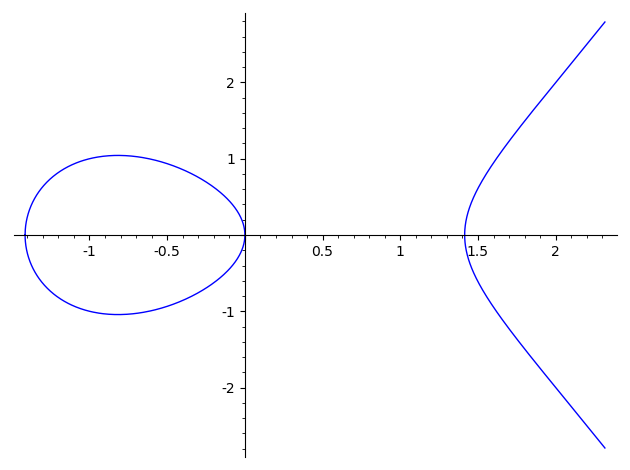
有限体 $\mathbb{F}_{23}$ 上

\(y^2 \equiv x^3 - 2x + 0 \pmod{23}\)

EllipticCurve(GF(23), [-2,0]).plot()

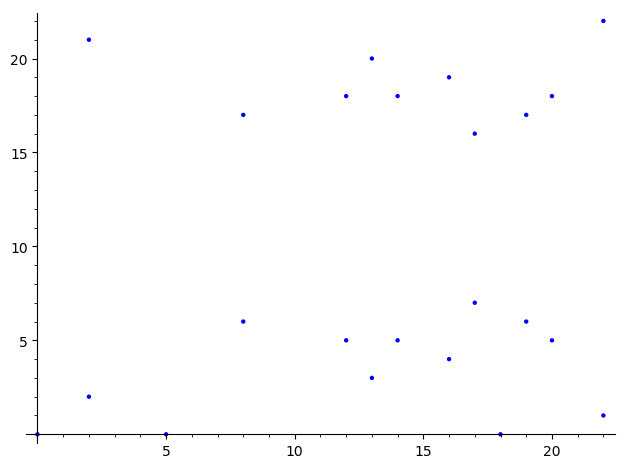
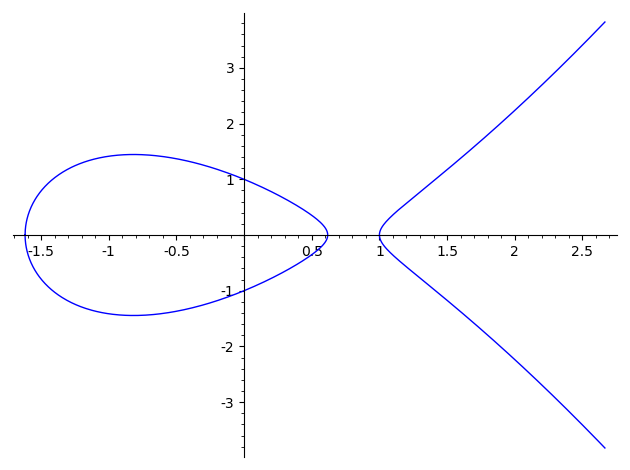
楕円曲線 $y^2 \equiv x^3 - 2x + 1$

$a=-2,\;b=1$ のときの、グラフ描画用のSageMathコードと、結果のグラフを示します。

実数体 $\mathbb{R}$ 上

EllipticCurve([-2,1]).plot()

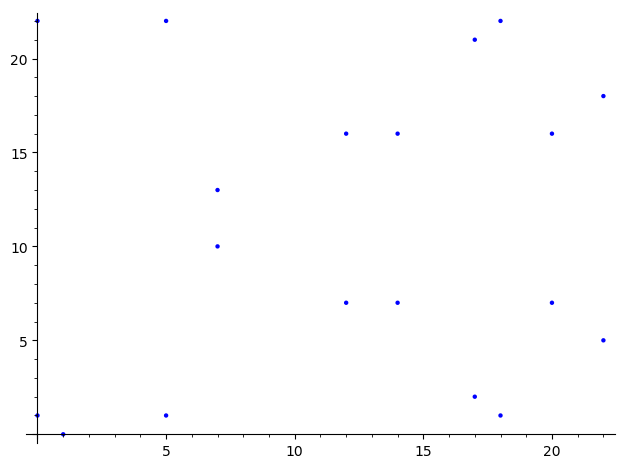
有限体 $\mathbb{F}_{23}$ 上

\(y^2 \equiv x^3 - 2x + 1 \pmod{23}\)

EllipticCurve(GF(23), [-2,1]).plot()

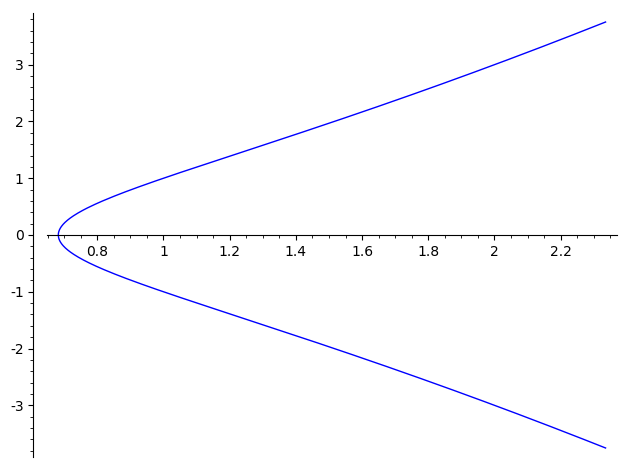
楕円曲線 $y^2 \equiv x^3 + x - 1$

$a=1,\;b=-1$ のときの、グラフ描画用のSageMathコードと、結果のグラフを示します。

実数体 $\mathbb{R}$ 上

EllipticCurve([1,-1]).plot()

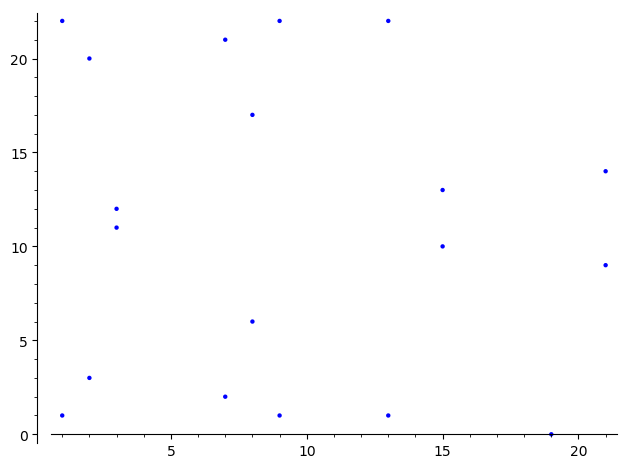
有限体 $\mathbb{F}_{23}$ 上

\(y^2 \equiv x^3 + x - 1 \pmod{23}\)

EllipticCurve(GF(23), [1,-1]).plot()

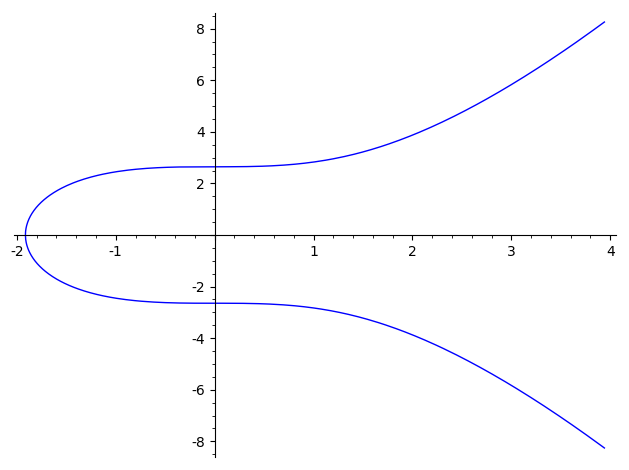
楕円曲線 $y^2 \equiv x^3 + 0x + 7$

$a=0,\;b=7$ のときの、グラフ描画用のSageMathコードと、結果のグラフを示します。

実数体 $\mathbb{R}$ 上

EllipticCurve([0,7]).plot()

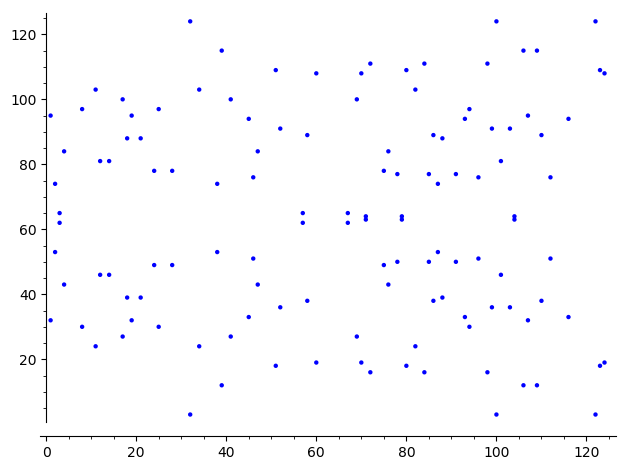
有限体 $\mathbb{F}_{127}$ 上

\(y^2 \equiv x^3 + 0x + 7 \pmod{127}\)

EllipticCurve(GF(127), [0,7]).plot()

SageMath で plot した画像を保存する

補足ですが、SageMath でプロットしたグラフを保存するには save メソッドを使います。

EllipticCurve(GF(127), [0,7]).plot().save('/path/to/file.png')